Use GA to solve TSP + Mini Project
A somewhat cryptic but intentional title, but for people knowing the lingo, this is a problem that could be solved using GA which stands for Genetic Algorithms and our problem TSP stand for Traveling Salesman Problem.
The Traveling Salesman Problem has been around for hundreds of years and I first heard of the problem over the summer when I was reading a book called ‘Algorithms to live by’ which was an interesting read which I can really recommend.
Here is a brief explanation of the problem.
The Travelling Salesman Problem describes a salesman who must travel to X amount of cites.
The order of which he does this does not matter, the only thing that matters is that he only visits each city once and that he finish where he started.
This problem is regarded as a very hard problem to solve, it’s also called a NP-hard problem by computer scientists.
I found it very interesting to approach solving this problem by using GA and I will try throughout this post to describe the approach of solving this problem using GA which is based on our last week assignment. t
Our first step is initialization, where we create our population which will be the distance to every city.
Here is the list of distances given to us in the lab:
Brighton
|
Bristol
|
Cambridge
|
Glasgow
|
Liverpool
|
London
|
Manchester
|
Oxford
| |
Brighton
|
0
|
172
|
145
|
607
|
329
|
72
|
312
|
120
|
Bristol
|
0
|
192
|
494
|
209
|
158
|
216
|
92
| |
Cambridge
|
0
|
490
|
237
|
75
|
205
|
100
| ||
Glasgow
|
0
|
286
|
545
|
296
|
489
| |||
Liverpool
|
0
|
421
|
49
|
208
| ||||
London
|
0
|
249
|
75
| |||||
Manchester
|
0
|
194
| ||||||
Oxford
|
0
|
In my code the 2D vector of all the distances looks like this:
vector<vector<int>> cities = {
{0, 172,145,607,329,72, 312,120},
{172,0, 192,494,209,158,216,92},
{145,192,0, 490,237,75, 205,100},
{607,494,490,0, 286,545,296,489},
{329,209,237,286,0, 421,49, 208},
{72, 158,75, 545,421,0, 249,75},
{312,216,205,296,49, 249,0, 194},
{120,92, 100,489,208,75, 194,0}
};
The next step is to evaluate every member in our population. The fitness of each individual in our population will be calculated on how good their fitness is, which in this case is total distance.
Next we do our selection. Our goal is to constantly improve the fitness of our population. The selection part will help us do just that. By using selection we will dispose of bad solution and keep the best solutions. We want to make sure that our most fittest individuals will be selected to pass on his genes to the next generation.
When using GA we're trying to simulate how natural selection is selecting the most suitable individual. As mention in my last post we will use the two core methods which are mutation and crossover.
With mutation, we are making a new individual but we slightly change/altering its chromosomes by random to hopefully get a better fitness for the next generation.
Here is my mutate function:s
//--------------------------------------------------------------
void Chrome::mutate(){
//----------------------------------------------------------
// generate random numbers
//----------------------------------------------------------
int randNum1, randNum2, temp;
randNum1 = floor(ofRandom((float)strand.size()));
randNum2 = floor(ofRandom((float)strand.size()));
//---------------------------------------------------------
// make sure it's not the same
//----------------------------------------------------------
while(randNum1 == randNum2){
randNum2 = floor(ofRandom((float)strand.size()));
}
temp = strand[randNum1];
strand[randNum1] = strand[randNum2];
strand[randNum2] = temp;
}
When applying crossover, it will create new individuals by combining genes of our selected individual. By doing this, we hope that we will be able to combine the best chromosomes from two individuals and make a child with a potentially better fitness for our selected problem which is to find the shortest possible total distance.
Here is my crossover function:
//--------------------------------------------------------------
vector<Chrome> ofApp::crossover(Chrome _one, Chrome _two){
//----------------------------------------------------------
// assign two parents & two children
//----------------------------------------------------------
vector<int> childOne = { -1, -1, -1, -1, -1, -1, -1, -1 };
vector<int> childTwo = { -1, -1, -1, -1, -1, -1, -1, -1 };
vector<int> parentOne = _one.getChromeStrand();
vector<int> parentTwo = _two.getChromeStrand();
//----------------------------------------------------------
// set random crossover point
//----------------------------------------------------------
int crossPoint = floor(ofRandom(1, 7));
//----------------------------------------------------------
// transfer everything right of crossover point
// from parent to child strands
//----------------------------------------------------------
for(int i = crossPoint; i < childOne.size(); i++){
childOne[i] = parentOne[i];
childTwo[i] = parentTwo[i];
}
int replaceIndex = 0;
//----------------------------------------------------------
// if the number is unique then it will be added to
// the child strand in correct order
//----------------------------------------------------------
for(int i = 0; i < parentOne.size(); i++){
if(!isInStrand(parentOne[i], childTwo)){
childTwo[replaceIndex ++] = parentOne[i];
}
}
replaceIndex = 0;
//----------------------------------------------------------
// repeat for 2nd parent
//----------------------------------------------------------
for(int i = 0; i < parentTwo.size(); i++){
if(!isInStrand(parentTwo[i],childOne)){
childOne[replaceIndex++] = parentTwo[i];
}
}
//----------------------------------------------------------
// create new vector with two sets of child chromosomes
//----------------------------------------------------------
vector<Chrome> childChromes;
childChromes.push_back(Chrome(childOne));
childChromes.push_back(Chrome(childTwo));
return childChromes;
}
These steps are being repeated and for every generation until we find the fittest individual for problem.
My final result is 890 miles and the best route is 0, 5, 2, 7, 1, 6, 4, 3.
This week we spent the lecture listening to everyones presentations regarding their upcoming mini project for this course.
I found a lot of value in listening to everybody and it's very interesting to hear everybody's ideas. Everyone seemed to have a unique idea even though we are all taking the same course and doing the same coursework. I found that to be very cool and I am very interested in seeing what everybody will make in the end.
My mini project for this course will be an application that will be trying to recreate sound using DFO.
The idea is to create a synthesizer that generate fairly simple sounds, then the user will create a sound that they like using the synthesiser, by clicking a button, the application will take a "snapshot" of the FFT of the created sound and now when the snapshot is created my DFO swarm will now try tro recreate the snapshot.
My search space in my application will be the FFT spectrogram of the synthesised sound.
My DFO swarm will search through the FFT and they will change the parameters in my synth in order to retrace the desired sound.
This approach will be a great tool for experimentation in trying to find a desired sound but it could also be fun to experiment with results such as trying to find the opposite sound, the sound that is the furthest away from the desired sound.
So each agent in my swam will act like a type of slider of the synthesiser and each agent will have its own fitness which will be how accurate or close the parameters are to the desired sound's FFT.
All the agents will be initialsed at a random value and then try to solve my problem.
This optimisation will happen in real time and and there will be a lot of sounds being synthesised. This could be an interesting thing to visualise by passing the different fitness values to a shader and create a unique visual experience.
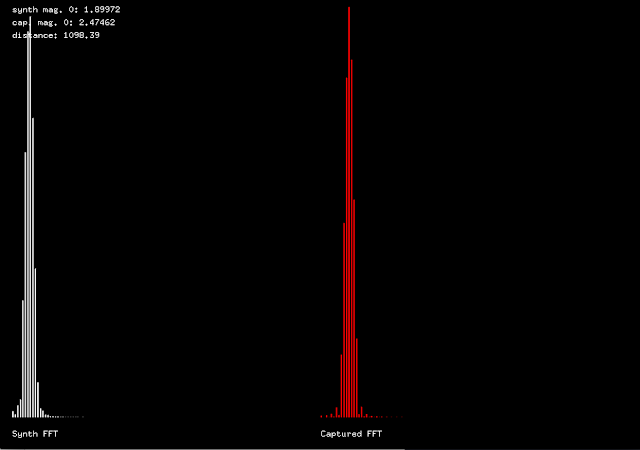
Here is an image that is showing a captured FFT of our desired sound and I am measuring the distance using Euclidean distance between both their FFT magnitudes. This is still early stage and I will start adding DFO by the end of this week.
MINI PROJECT
This week we spent the lecture listening to everyones presentations regarding their upcoming mini project for this course.
I found a lot of value in listening to everybody and it's very interesting to hear everybody's ideas. Everyone seemed to have a unique idea even though we are all taking the same course and doing the same coursework. I found that to be very cool and I am very interested in seeing what everybody will make in the end.
My mini project for this course will be an application that will be trying to recreate sound using DFO.
The idea is to create a synthesizer that generate fairly simple sounds, then the user will create a sound that they like using the synthesiser, by clicking a button, the application will take a "snapshot" of the FFT of the created sound and now when the snapshot is created my DFO swarm will now try tro recreate the snapshot.
My search space in my application will be the FFT spectrogram of the synthesised sound.
My DFO swarm will search through the FFT and they will change the parameters in my synth in order to retrace the desired sound.
This approach will be a great tool for experimentation in trying to find a desired sound but it could also be fun to experiment with results such as trying to find the opposite sound, the sound that is the furthest away from the desired sound.
So each agent in my swam will act like a type of slider of the synthesiser and each agent will have its own fitness which will be how accurate or close the parameters are to the desired sound's FFT.
All the agents will be initialsed at a random value and then try to solve my problem.
This optimisation will happen in real time and and there will be a lot of sounds being synthesised. This could be an interesting thing to visualise by passing the different fitness values to a shader and create a unique visual experience.
Here is an image that is showing a captured FFT of our desired sound and I am measuring the distance using Euclidean distance between both their FFT magnitudes. This is still early stage and I will start adding DFO by the end of this week.


Comments
Post a Comment